This is part of an ongoing series where we write a complete 2D game engine in C++ and SFML. A new tutorial is released every Monday. You can find the complete list of tutorials here and download the source code from the projects GitHub page.

Last week we discussed what we want from our collision system and started work on a collidable component, which is a great start but now we need some way to store the collidable objects. We could just use a vector and check if every object is colliding with every other object but that’s not ideal and will quickly slow our game down by performing hundreds of unnecessary and often expensive collision checks*. So we need a data structure that is in some way aware of the position of the object in the world, which, as no one who read the title of the tutorial will be surprised by, is where the quadtree comes in.

*Although currently we only have a few tiles and our player in our game and will only be performing the relatively quick rectangular intersection checks. This will change as we progress with our game and add more objects which in turn may require more detailed collision checks.

So what exactly is a quadtree? Let’s start by looking at what Wikipedia has to say on the subject.

A quadtree is a tree data structure in which each internal node has exactly four children. …most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions.

The bit that we’re interested in is the quadtrees ability to ‘partition a two-dimensional space by recursively subdividing it into four quadrants or regions.’ We’ll look at what that means in a bit more detail.Our quadtree will start as one node. When we add an object to our game (we’ll use the player as an example), it will be added to this root or parent node.


Quadtree with one player object

At this point, our tree has one level which contains our one object. As we continue to add objects to the game the node will pass a threshold (set by us) and will split into four child nodes or as Wikipedia puts it, it is: ‘recursively subdividing into four quadrants’.


Quadtree subdivided into four quadrants

Our original node has split into four quadrants.

Now, whenever we attempt to add an object to our parent node it will calculate which of the four child nodes to place the object in.As we add more objects the nodes can split further.


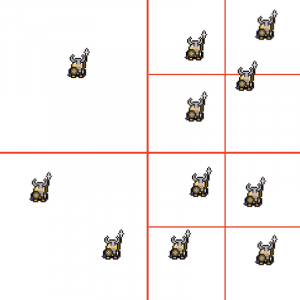
Quadtree nodes have split further as we add objects.

The quad trees nodes have split again as we add more objects.

If an object does not fit within a child nodes boundary (as shown in the top right node in the image above) it is placed in the parent node.As we add more objects into our quadtree it will continue to divide up until a predefined limit. An example of what a quadtree could look like in our existing game if we added 200+ players is shown below.


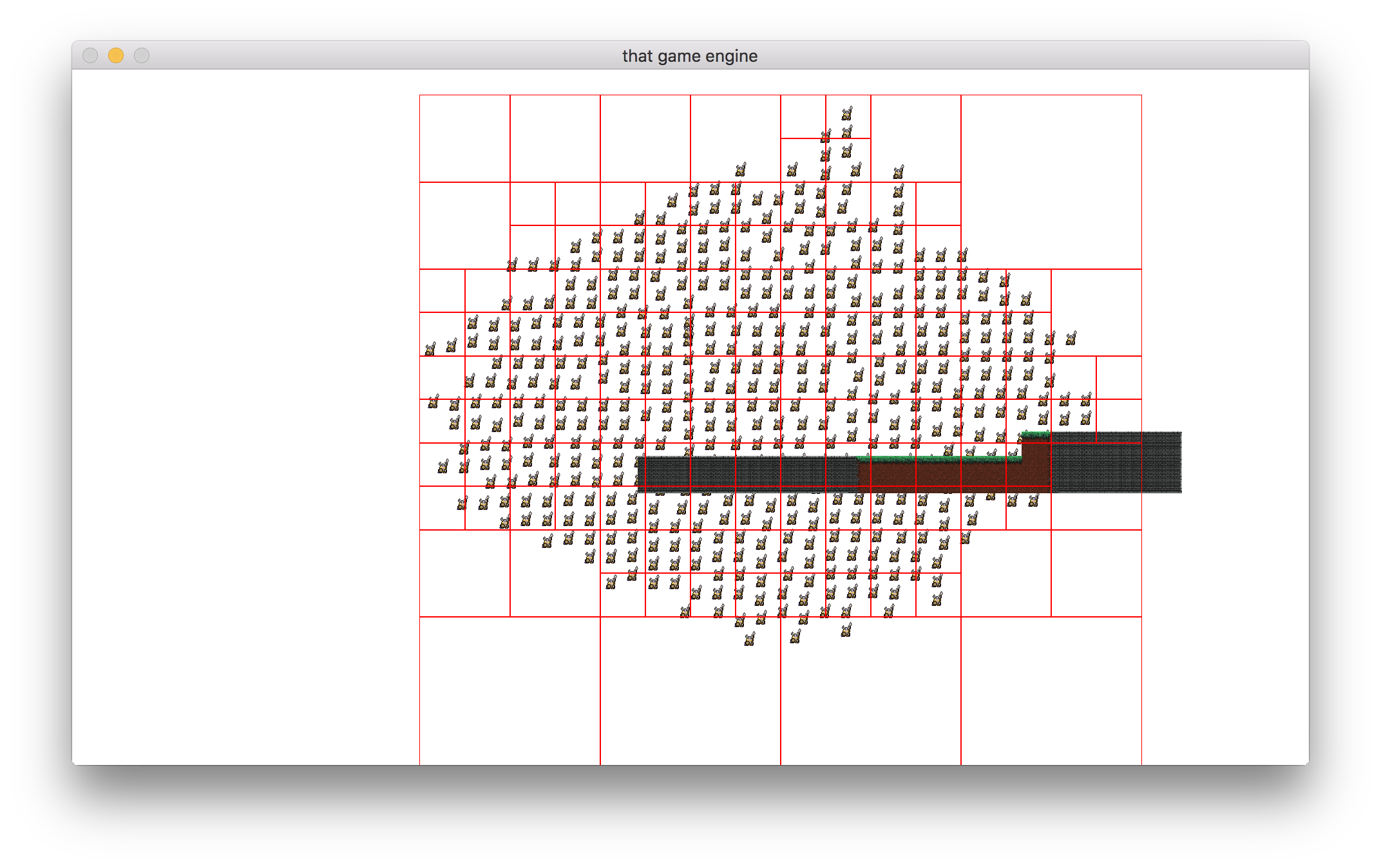
Example quadtree implementation with 200+ players.
Example quadtree implementation with 200+ players.

Each node only contains a couple of the player objects and we would only need to perform collision checks on objects that are within the same node or in an adjacent node to the area we provide. This dramatically reduces the number of collision checks we will need to perform.

One caveat to the quadtree that we are going to write is that as many of the objects will be moving around the environment, they will not always stay within the node they were initially placed in. One way of working around this is to remove and re-add all objects every single frame. While this may sound like a significant drawback it is still quicker to do this than to check if every object is colliding with every other object. We may also look at a different method where we can update an object’s node within the quadtree only when they move, but we’ll only do that if we run into performance issues.

To query our quadtree we will pass it the rectangular area of the object we are performing collision checks on. Even when we implement different collision shapes in future it may be a good idea to leave this as a rectangular area so that the quadtree can perform quick collision checks and return a vector of possible collisions which we can then perform more complicated checks on if necessary.



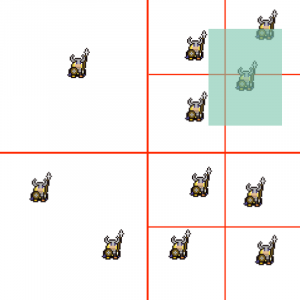
An example search performed on our quadtree.

Let’s imagine that the green rectangle in the image above represents the area of a baddie that we’ve just spawned into the game. I want to know if it’s colliding with any player objects so I can apply damage to them and knock them out of the way, so I query the quadtree with this baddies area. Now rather than having to check if our baddie is colliding with all other objects in the level, it will notice that the search area only intersects with four nodes and will then check the objects within those four nodes to see if they are colliding (reducing the number of collision checks from 11 to 4).

So hopefully you have a better idea of what a quadtree is and how it will help us. If not then firstly sorry! And secondly, there are some great tutorials that go through it in a bit more detail. I personally love the interactive explanation that you can find here.

With the theory out of the way, there are a couple of things we need to do before we can implement our own quadtree. We need to create a new component that will store a unique id for each object. We’ll use this to quickly tell if two objects are different. And we also need to make the pointer to Object in our Component class public so that when we have a reference to an objects component we can also access its owner. We’ll start with the latter first as its a quick change.

Component.hpp 
class Component
{
public:
…
    // Moved owner so that it is public.
    Object* owner;
};
You can, of course, create a getter for it instead, which is probably what most people will prefer to do. I won’t get into the debate about whether to use accessors and mutators or not as firstly I’m not sure how I feel about them and secondly, sometimes I use them (as you’ll see in the next code example when we create our id component).You can, of course, create a getter for it instead, which is probably what most people will prefer to do. I won’t get into the debate about whether to use accessors and mutators or not as firstly I’m not sure how I feel about them and secondly, I often use them, as you’ll see right now because we’re going to create an id component.
C_InstanceID.hpp 
#ifndef C_InstanceID_hpp
#define C_InstanceID_hpp

#include "Component.hpp"

class C_InstanceID : public Component
{
public:
    C_InstanceID(Object* owner);
    ~C_InstanceID();
    
    int Get() const;
    
private:
    static int count;
    int id;
};

#endif /* C_InstanceID_hpp */
C_InstanceID.cpp 
#include "C_InstanceID.hpp"

int C_InstanceID::count = 0;

C_InstanceID::C_InstanceID(Object* owner) : Component(owner), id(count++){}

C_InstanceID::~C_InstanceID(){}

int C_InstanceID::Get() const
{
    return id;
}
This component simply stores a unique id and provides an accessor so we can retrieve an objects id. When we create the instance id component it increments a static count variable so that every instance will have a different id. We want every object to have an id so we’ll add a pointer to one in the object’s header and instantiate it in the object’s constructor.
Object.hpp 
class Object
{
public:
…
    std::shared_ptr<C_InstanceID> instanceID;
};

Object.cpp 
Object::Object() : queuedForRemoval(false)
{
    transform = AddComponent<C_Transform>();
    instanceID = AddComponent<C_InstanceID>();
}

And that’s it for the small changes, we can now start work on our quadtree. I’ll be adapting the quadtree found here.

There will only be the one class for our quadtree, I unsurprisingly called it Quadtree (once I’d realised quadtree was one word and renamed it from QuadTree that is).

Quadtree.hpp 
#ifndef QuadTree_hpp
#define QuadTree_hpp

#include <memory>
#include <vector>

#include "C_BoxCollider.hpp"
#include "Object.hpp"

class Quadtree
{
public:
    Quadtree();
    Quadtree(int maxObjects, int maxLevels, int level, 
			 sf::FloatRect bounds, Quadtree* parent);
    
	// Inserts object into our quadtree.
    void Insert(std::shared_ptr<C_BoxCollider> object);
	
	// Removes object from our quadtree when we no longer need it to collide.
    void Remove(std::shared_ptr<C_BoxCollider> object);
	
	// Removes all objects from tree.
    void Clear();
    
	// Returns vector of colliders that intersect with the search area.
    std::vector<std::shared_ptr<C_BoxCollider>> 
		Search(const sf::FloatRect& area);
    
	// Returns the bounds of this node.
    const sf::FloatRect& GetBounds() const;
    
private:
	void Search(const sf::FloatRect& area,
	std::vector<std::shared_ptr<C_BoxCollider>>&
	overlappingObjects);

	// Returns the index for the node that will contain 		
	// the object. -1 is returned if it is this node.
    int GetChildIndexForObject(const sf::FloatRect& objectBounds);

	// Creates the child nodes.
    void Split();
    
	// We’ll use these as indices in our array of children.
    static const int thisTree = -1;
    static const int childNE = 0;
    static const int childNW = 1;
    static const int childSW = 2;
    static const int childSE = 3;
    
    int maxObjects;
    int maxLevels;
    
	// nulptr is this is the base node.
    Quadtree* parent;
    std::shared_ptr<Quadtree> children[4];
    
	// Stores objects in this node.
    std::vector<std::shared_ptr<C_BoxCollider>> objects; 
    
	// How deep the current node is from the base node. 
	// The first node starts at 0 and then its child node 	
	// is at level 1 and so on.
    int level;
    
	// The bounds of this node.
    sf::FloatRect bounds;
};

#endif /* QuadTree_hpp */

That may seem like a lot at first but our quadtree really only has four public functions (excluding GetBounds, which is just an accessor for the node’s bounds) and they are: insert, remove, clear, and search. Hopefully, the names are self-explanatory: insert, remove, and clear allow us to add and remove objects to and from the tree; while search provides a way of querying the tree, we’ll provide a rectangular area that we’re interested in and the tree will return a vector of objects that intersect that area. We’ll start the implementation by writing the constructors.
Quadtree.cpp 
#include "Quadtree.hpp"

Quadtree::Quadtree() : Quadtree(5, 5, 0, {0.f, 0.f, 1920, 1080}, 
								nullptr){}

Quadtree:: Quadtree(int maxObjects, int maxLevels, int level, 
					sf::FloatRect bounds, Quadtree* parent) 
					: maxObjects(maxObjects), maxLevels(maxLevels), 
					level(level), bounds(bounds), parent(parent){}
Here we provide a default constructor, which we’ll use when first creating the quadtree and another constructor where we can set the quadtrees variables, which we’ll use when we create child nodes.

So what are we passing into the constructor:

  • maxObjects: how many objects a node can contain before it splits into child nodes.
  • maxLevels: starting from the base node (0) how many times can it (and its children) split.
  • level: this is the current level of the tree. This is set to 0 in the default constructor as it is the base node.
  • bounds: the area of the quadtree. This controls the position and size of the tree.
  • parent: if this is a child node then parent node is included here, otherwise this will be a nulptr.

Quadtree nodes have split further as we add objects.


 This quadtree has 3 levels, level 0 is the whole area, level 1 is the first big split, level 2 are the smaller splits in the top-right and bottom-right quadrants.


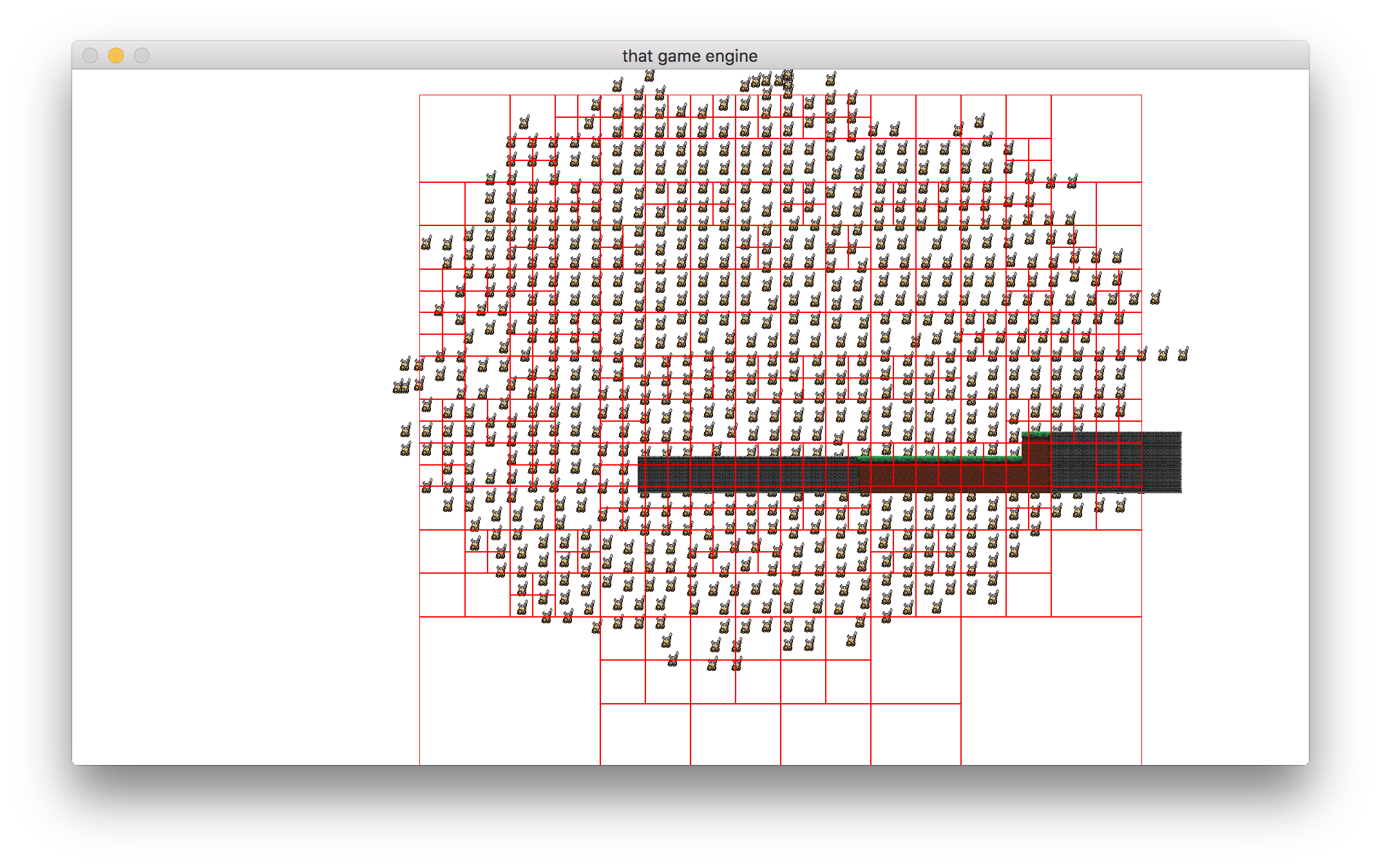
The size of the quadtree is very important because objects outside of this space will not be included in our collision system and will therefore not collide.

The size of the quadtree is very important because objects outside of this space will not be included in our collision system and will therefore not collide. As you can see from the image above there are a number of objects bunched at the top of the screen that are technically colliding but nothing is being done about it because they are outside the bounds of the quadtree.Next up is the insert method. With a quadtree, we can’t just add the object to a nodes collection we need to perform a couple of extra steps to make sure we are inserting the object into the right node.

Quadtree.cpp 
void Quadtree::Insert(std::shared_ptr<C_BoxCollider> object)
{
    if(children[0] != nullptr) // 1
    {
        int indexToPlaceObject = 
			GetChildIndexForObject(object->GetCollidable()); // 2
        
        if(indexToPlaceObject != thisTree) // 3
        {
            children[indexToPlaceObject]->Insert(object);
            return;
        }
    }
    
    objects.emplace_back(object); // 4
    
    if(objects.size() > maxObjects && 
	   level < maxLevels && children[0] == nullptr) // 5
    {
        Split(); // 6
        
        auto objIterator = objects.begin(); // 7
        while (objIterator != objects.end())
        {
            auto obj = *objIterator;
            int indexToPlaceObject = 
				GetChildIndexForObject(obj->GetCollidable());
            
            if (indexToPlaceObject != thisTree)
            {
                children[indexToPlaceObject]->Insert(obj);
                objIterator = objects.erase(objIterator);
            
            }
            else
            {
                ++objIterator;
            }
        }
    }
}

Let’s break the function down into its separate steps:

  1. It first needs to check if it has any children nodes. We assume if the first child node is present then all four nodes are because when we split the node we create the four children together.
  2. If this node has child nodes then we call a function (that we have not yet written) whose job is to return the index of the node that the object should belong to.
  3. If the function returns an index to a child node and not to this node then we call the child nodes insert function and return.
  4. At this point, we know that this node has no child nodes so we insert the object into this nodes collection.
  5. As we’ve added a new object we need to check if we have exceeded the maximum number of objects allowed in a node.
  6. If we exceed the object count limit we need initialise child nodes.
  7. And lastly, once we’ve split into child nodes we need to iterate over every object in this node and calculate if it should be in a child node instead.

With inserting objects complete we’ll write the removal function next. We’ll want to remove an object from the quadtree when we no longer want them colliding with other objects i.e. when a projectile collides with an object we want to remove it from quadtree so we no longer perform collision checks on it.

Quadtree.cpp 
void Quadtree::Remove(std::shared_ptr<C_BoxCollider> object)
{
    int index = GetChildIndexForObject(object->GetCollidable());
    
    if(index == thisTree || children[index] == nullptr)
    {
        for(int i = 0; i < objects.size(); i++)
        {
            if(objects.at(i)->owner->instanceID->Get() 
			   == object->owner->instanceID->Get())
            {
                objects.erase(objects.begin() + i);
                break;
            }
        }
    }
    else
    {
        return children[index]->Remove(object);
    }
}
Removing an object is straightforward: we first check if the object belongs to this node and if it does we loop through all objects belonging to this node to find the object with the same id (using the instance id component we wrote at the beginning of this weeks tutorial) and then, if found, its erased from the collection. If the object belongs to a child node we call remove on that node instead.To clear the quadtree of all of its objects we clear the object vector of this node and then do the same for any children nodes.
Quadtree.cpp 
void Quadtree::Clear()
{
    objects.clear();
    
    for(int i = 0; i < 4; i++)
    {
        if(children[i] != nullptr)
        {
            children[i]->Clear();
            children[i] = nullptr;
        }
    }
}

And I think I’ll leave it here for this week. I was hoping to finish the quadtree in this tutorial but it proved to be too big of a topic. Next week we’ll write the all-important search function (there’d be no point in our tree if we couldn’t search it) and finish with a few of the helper functions. And the week after that we’ll create the collision system that will make use of the quadtree.

As always, if you have any suggestions for what you would like covered or are having any trouble implementing a feature, then let me know in the comments and I’ll get back to you as soon as I can. Thank you for reading 🙂