This is part of an ongoing series where we write a complete 2D game engine in C++ and SFML. A new tutorial is released every Monday. You can find the complete list of tutorials here and download the source code from the projects GitHub page.
Last week we started work on the data structure that will store all of the objects that we want to be colliding. The quadtree will store our collidables spatially to help us minimise the number of collision calls we need to make. If you would like a refresher on the theory behind quadtrees then see my previous tutorial here. This week we will finish the quadtree by implementing: search functionality, the ability to split a parent node to create children nodes, and a few other helper functions.
As the quadtree was explained in detail last week, we can jump right into the code. We’ll start by writing the search function. This is the function that our collision system (which we’ll start next week) will call. It returns a vector of objects that intersect the area we have passed in. So let’s say that we pass in the area of our player, it will return any objects that are also in that area, we can then move them out of the player bounds, apply damage to the player, and do whatever else we need to. You may have noticed that there are two search functions: one that returns a vector (the public function) and one that returns void (private to the quadtree). In reality, there are three main steps to retrieving objects from our quadtree.
Step 1: we pass a search area to the quadtree. This area would normally coincide with the collision box of an existing object i.e. the player. This is a call to the public search function.
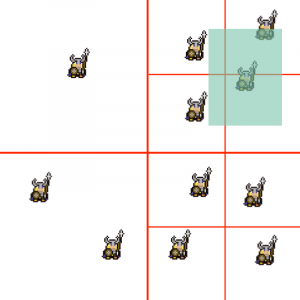
The green rectangle represents our search area.
Step 2: the public function will call the private search function. This private function will then add all the objects from any nodes that intersect the search tree to a vector. In this example, it will return a vector of 4 objects.
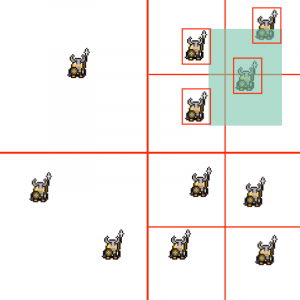
First the quadtree builds a vector with all of the objects from any node that intersects our search area.
Step 3: back in the public function the quadtree will iterate over all of the objects from these nodes and check which objects actually intersect the search area. Only the objects that intersect the area are returned from the search function. In this simple example the quadtree has reduced the number of collision checks from 11 (needing to check if its colliding with every other object) to 4 (only needing to check if it’s colliding with the objects in the nodes that intersect the search area). In the final game, we may have hundreds of possible collision objects so you can imagine how many collision checks the quadtree will help save each frame.
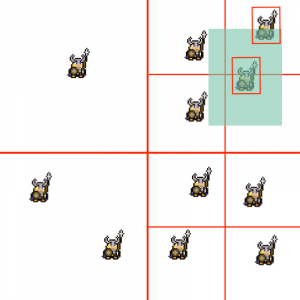
The quadtree returns these two objects as they intersect the search area.
std::vector<std::shared_ptr<C_BoxCollider>> Quadtree::Search(const sf::FloatRect& area)
{
std::vector<std::shared_ptr<C_BoxCollider>> possibleOverlaps; // 1
Search(area, possibleOverlaps); // 2
std::vector<std::shared_ptr<C_BoxCollider>> returnList;
for (auto collider : possibleOverlaps)
{
if (area.intersects(collider->GetCollidable())) // 3
{
returnList.emplace_back(collider); // 4
}
}
return returnList;
}
The function performs the following steps:
- Creates a vector to hold all objects that may be overlapping with our search area.
- Calls the private search function, passing it the vector as a reference (we’ll write this next). This function fills the vector with all of the objects in the nodes that intersect with our search area.
- As our area may not necessarily intersect with all of the objects in the returned nodes, we then need to iterate over all of these possible overlaps and performs a rectangle intersection check. We do this check because it is quick, if we require more detailed collision checks we would perform them in our collision system.
- If the object is intersecting with our search area we add it to the vector of objects that are returned from this function.
This is mostly straightforward as much of the work actually happens in the call to the private search function. void Quadtree::Search(const sf::FloatRect& area,
std::vector<std::shared_ptr<C_BoxCollider>>& overlappingObjects)
{
overlappingObjects.insert(overlappingObjects.end(), objects.begin(), objects.end()); // 1
if(children[0] != nullptr)
{
int index = GetChildIndexForObject(area); // 2
if(index == thisTree) // 3
{
for(int i = 0; i < 4; i++)
{
if(children[i]->GetBounds().intersects(area))
{
children[i]->Search(area, overlappingObjects);
}
}
}
else // 4
{
children[index]->Search(area, overlappingObjects);
}
}
}
We’ll go through this method step by step as well:
- It starts by adding all the objects in this node to the vector. As you’ll remember from the beginning of this tutorial this will contain either all the objects that do not fit neatly into a child node (if there are child nodes) or it will contain all the objects that fit within this node if there are no child nodes.
- Retrieves the child index for the search area. This function will either return a -1 to signify that the search area does not fit into a child node completely (or there are no child nodes) or it will return an index to the child node that contains the area.
- If it returns an index to this tree and we have children nodes then we need to call the search functions for any child node that intersects with our area to make sure that we have added all objects that could possibly be intersecting our area.
- If it returns an index to a child node then we need to call that child nodes search function.
const sf::FloatRect& Quadtree::GetBounds() const
{
return bounds;
}
Not much needs to be said about that. It simply returns the rect for this nodes bounds. We use this when deciding if a search area intersects the node and also for deciding if an object fits within a node. We only have two more functions to write before our quadtree is complete: GetChildIndexForObject and Split. Lets start with GetChildIndexForObject. We’ve called this function a couple of times in our code: when we’re working out where to place an object, and when we’re trying to find an object and we want to know which node to search. Its job is to accept an area and then to calculate if that area can be contained completely within a child node, if so it will return an index to that child node, or if the area overlaps a number of child nodes it will then return this index of the current node instead.
int Quadtree::GetChildIndexForObject(const sf::FloatRect& objectBounds)
{
int index = -1;
double verticalDividingLine = bounds.left + bounds.width * 0.5f;
double horizontalDividingLine = bounds.top + bounds.height * 0.5f;
bool north = objectBounds.top < horizontalDividingLine
&& (objectBounds.height + objectBounds.top < horizontalDividingLine);
bool south = objectBounds.top > horizontalDividingLine;
bool west = objectBounds.left < verticalDividingLine
&& (objectBounds.left + objectBounds.width < verticalDividingLine);
bool east = objectBounds.left > verticalDividingLine;
if(east)
{
if(north)
{
index = childNE;
}
else if(south)
{
index = childSE;
}
}
else if(west)
{
if(north)
{
index = childNW;
}
else if(south)
{
index = childSW;
}
}
return index;
}
It performs four checks to see if the provided area is totally contained within the north, south, east, or west of this nodes bounds. It then uses those checks to see if the area will fit within a child nodes bounds.The last function we are going to write today is the one that will ‘split’ this node into four child nodes. We still keep the parent node (which will be used to hold any objects that do not fit entirely within a child nodes bounds).
void Quadtree::Split()
{
const int childWidth = bounds.width / 2;
const int childHeight = bounds.height / 2;
children[childNE] = std::make_shared<Quadtree>(maxObjects, maxLevels, level + 1,
sf::FloatRect(bounds.left + childWidth, bounds.top, childWidth, childHeight),
this);
children[childNW] = std::make_shared<Quadtree>(maxObjects, maxLevels, level + 1,
sf::FloatRect(bounds.left, bounds.top, childWidth, childHeight),
this);
children[childSW] = std::make_shared<Quadtree>(maxObjects, maxLevels, level + 1,
sf::FloatRect(bounds.left, bounds.top + childHeight, childWidth, childHeight),
this);
children[childSE] = std::make_shared<Quadtree>(maxObjects, maxLevels, level + 1,
sf::FloatRect(bounds.left + childWidth, bounds.top + childHeight, childWidth, childHeight),
this);
}
This instantiates four new quadtree objects and points them to the array using the static indices in the header. The bounds of each child are calculated as a subset of the parent’s bounds as shown below.
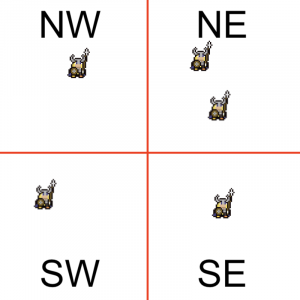
One parent node split into four child nodes.
And that’s it for this week, our quadtree is now complete! Next week we’ll be starting work on our new collision system which will make use of the quadtree.
As always, if you have any suggestions for what you would like covered or are having any trouble implementing a feature, then let me know in the comments and I’ll get back to you as soon as I can.
Thank you for reading 🙂